Explicamos o que é um diagrama de Venn, para que serve e seus elementos. Além disso, contamos quais tipos existem e como fazê-los.

O que é um diagrama de Venn?
O diagrama de Venn é um tipo de organizador gráfico que mostra como dois ou mais conjuntos de elementos estão relacionados, pois, Usando círculos sobrepostos, representa quais características eles compartilham e quais não. duas ou mais categorias, grupos, ideias, conceitos, teorias, entre outros.
No diagrama de Venn existem:
- um rectângulo. Representa o universo, ou seja, a totalidade dos elementos, e é designado com um título. Em alguns diagramas não há retângulo, mas há um título.
- Dois ou mais círculos. Representam conjuntos, ideias, conceitos ou categorias que são designados por um título ou frase.
- Palabras o frases. Representam os elementos de um conjunto, os membros de uma categoria ou de uma série de características.
- Uma sobreposição entre os círculos. Representa as ligações entre conjuntos, que podem ser interseção, inclusão ou disjunção.
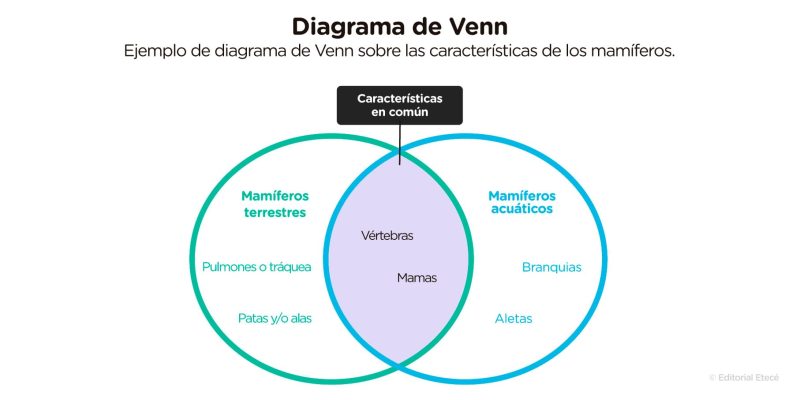
Por exemplo, num diagrama sobre mamíferos, o universo é características dos mamíferos e existem dois conjuntos: mamíferos terrestres sim mamíferos aquáticos. Em cada círculo são escritas as características compartilhadas pelos membros de cada turma e na superposição de ambos os círculos são anotadas as características comuns de ambos os conjuntos.
Pode ajudá-lo: Diagrama
Características do diagrama de Venn
Ao contrário da maioria dos organizadores gráficos, o diagrama de Venn permite:
- Identifique quais e quantos conjuntos existem em relação a um tópico.
- Mostre que ligação existe entre os conjuntos.
- Indique a qual conjunto cada elemento pertence e, em alguns casos, identifique os elementos que fazem parte de dois ou mais conjuntos.
- Determine que pode haver elementos que não pertencem a nenhum conjunto.
Para que serve o diagrama de Venn?
O diagrama de Venn apresenta grandes vantagens e é utilizado para diversos fins:
- Exibir informações visualmente. Ajuda a organizar as informações para que sejam mais fáceis de entender.
- Permite representar graficamente a relação entre dois ou mais conjuntos. É usado para ver quais características ou quais elementos dois ou mais conjuntos têm em comum e quais são suas diferenças.
- É útil para fazer classificações. É usado para determinar quais elementos pertencem a cada categoria.
- Permite comparações. Serve para contrastar características ou elementos de objetos, produtos, lugares, teorias, entre outros.
- É uma ferramenta para tomar decisões. Permite ver duas ou mais opções com mais clareza e refletir sobre qual é a mais conveniente.
Tipos de diagrama de Venn
Existem diferentes tipos de diagramas de Venn, dependendo do tipo de relação estabelecida entre os conjuntos:
Diagrama de Venn de interseção
Mostra que existem elementos que pertencem a um conjunto ou outro e elementos que pertencem a ambos. Pode haver dois ou mais círculos, dependendo de quantos conjuntos existem. Por exemplo:
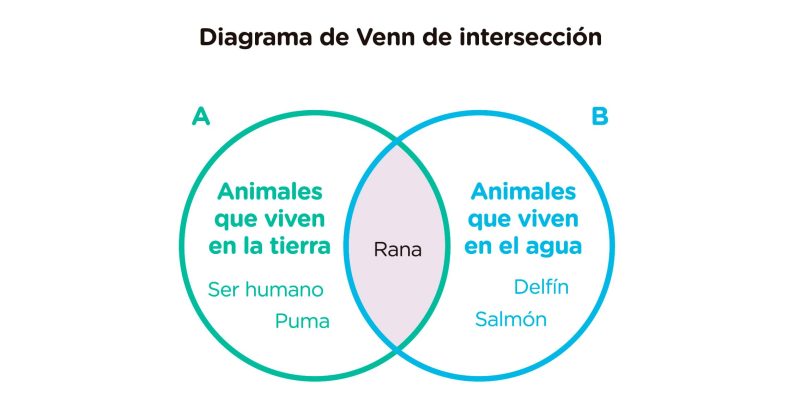
O elemento rana Está na encruzilhada, porque é um animal que vive tanto na terra quanto na água.
Diagrama de Venn de Inclusão
Mostra que um conjunto inclui um subconjunto. Por exemplo:
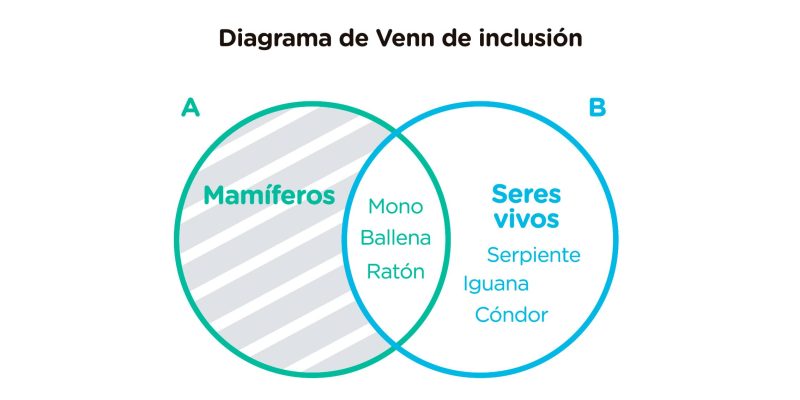
Conjunto B (seres vivos) inclui o subconjunto A (mamíferos), e, como não existem mamíferos que não sejam seres vivos, a parte do círculo está sombreada ou riscada mamíferos que não está incluído seres vivos. Além disso, o gráfico indica que existem outros seres vivos que não são mamíferos, como a cobra, a iguana e o condor.
Diagrama de Disjunção de Venn
Mostra que os conjuntos contêm elementos que não pertencem a outros conjuntos. Por exemplo:
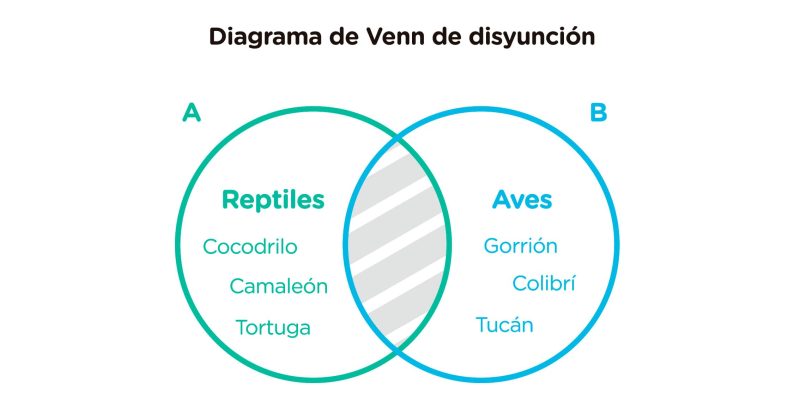
Os círculos sobrepostos estão sombreados ou riscados, para representar que nenhum elemento do conjunto répteis pode pertencer ao conjunto aves e vice-versa.
Como fazer um diagrama de Venn?
Para fazer um diagrama de Venn, você pode seguir uma série de etapas:
- Determine o tema. Você deve selecionar o tema e quais aspectos deseja comparar. Por exemplo, você pode comparar as características de dois carros.
- Anote todos os itens de uma lista. Você pode fazer um brainstorming para anotar todos os elementos ou características. Por exemplo, você pode escrever todas as características mais importantes dos carros em geral.
- Determine os conjuntos. Você deve determinar em quais conjuntos os elementos ou características irão e desenhar um círculo para cada conjunto. Se dois carros forem comparados, haverá dois círculos sobrepostos, um para o carro A e outro para o carro B.
- Indique qual elemento pertence a cada conjunto. Os elementos ou características devem ser anotados no conjunto correspondente. Se algum elemento ou característica pertencer a dois conjuntos, está escrito no setor onde os círculos se sobrepõem. Por exemplo, o recurso “rápido” só está presente no carro A, por isso será notado no primeiro círculo; A característica “confortável” só está presente no carro B, por isso estará escrita no segundo círculo; e o recurso “economia” for encontrado em ambos os carros, isso será anotado na sobreposição.
Exemplos de diagramas de Venn
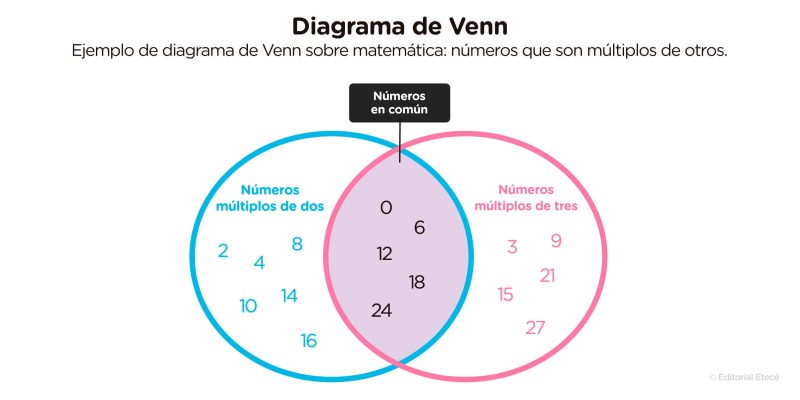
Neste diagrama, existem dois conjuntos: números múltiplos de dos sim números múltiplos de três. Em cada círculo anotam-se os números correspondentes e, na superposição, aqueles que são múltiplos de dois e três, ou seja, que pertencem aos dois conjuntos.
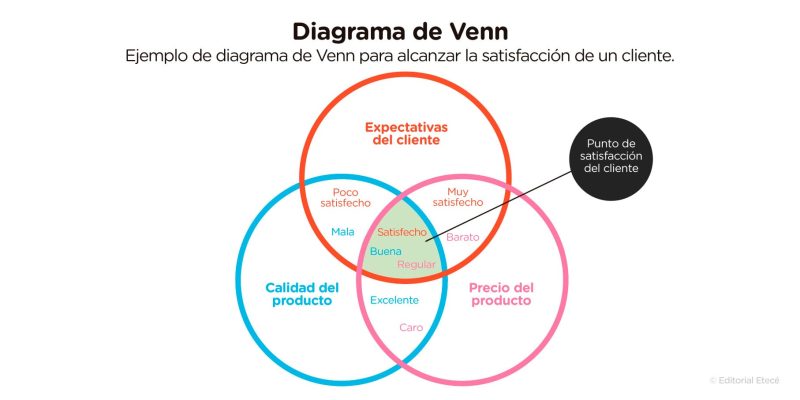
Neste diagrama, é medido o ponto de satisfação do cliente que é alcançado quando há um equilíbrio entre as expectativas do cliente, a qualidade do produto e o preço do produto.
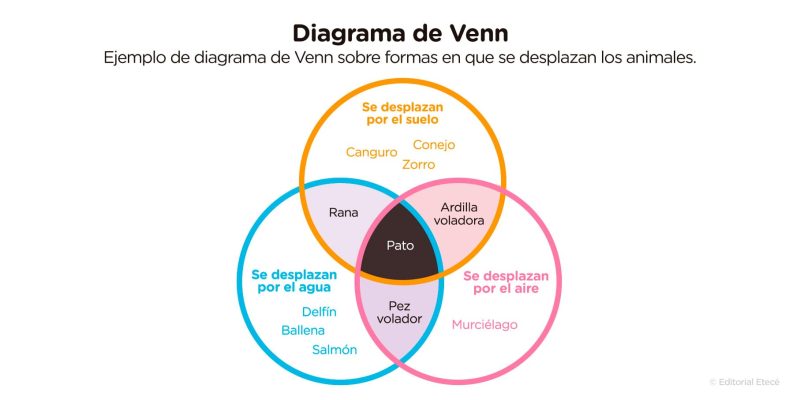
Neste diagrama, existem três conjuntos: animais que se movem na terra, animais que se movem na água sim animais que se movem pelo ar. Em cada círculo são anotados os animais que pertencem a uma classe e, nas interseções, aqueles que pertencem a dois ou mais conjuntos.
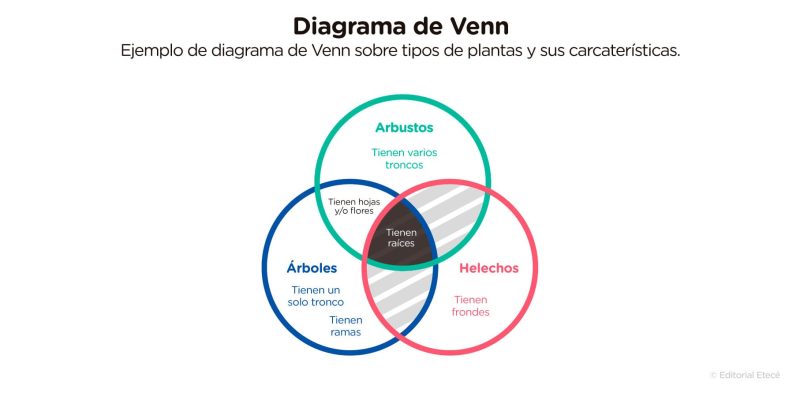
Neste diagrama, as características dos conjuntos são mencionadas arbustos, árvores sim samambaias. Nas intersecções são anotadas as características que dois ou mais tipos de plantas têm em comum. No entanto, as sobreposições de arbustos sim samambaias e de árvores sim samambaias Estão riscados porque não possuem características em comum.
Áreas em que o diagrama de Venn é usado
O diagrama de Venn é usado para diferentes propósitos dependendo da disciplina:
- Matemáticas. Serve para ensinar e aprender conjuntos numéricos e suas ligações de forma didática. Também é aplicado na resolução de equações e problemas e em análises probabilísticas.
- Estatisticas. É usado para comparar dados ao analisar como uma variável se manifesta em uma população.
- Lógica. Serve para representar proposições e analisar a validade dos argumentos.
- Ensino. É utilizado para classificar diferentes elementos e comparar teorias, conceitos e características em diversas disciplinas, como linguagem, literatura, ciências sociais e ciências naturais.
- Campo de negócios. É utilizado para analisar e comparar produtos, serviços, necessidades de clientes, processos produtivos, projetos, entre outros.
- Informática. É usado para analisar e comparar diferentes tipos de dados, como algoritmos e preferências e pesquisas do usuário.
Glossário do Diagrama de Venn
Os diagramas de Venn são usados para representar graficamente conjuntos e suas operações na teoria dos conjuntos. Nesta teoria são utilizados termos específicos, alguns dos mais importantes são:
- Universo. É aquilo que contém todos os elementos. Por exemplo, um universo pode ser composto por todos os números múltiplos de outros.
- Definir. É algo que contém um grupo de elementos que compartilham uma ou mais características. Por exemplo, em um diagrama existem dois conjuntos: números que são múltiplos de 3 sim números que são múltiplos de 4.
- conjunto vazio. É um conjunto que não contém nenhum elemento. Por exemplo, se o universo for todos os livros de uma biblioteca e não há livros de geografia, argumenta-se que livros de geografia É um conjunto vazio.
- Elemento. Ele é membro de um grupo. Por exemplo, 3, 6 e 9 são elementos do conjunto múltiplos de 3.
- Inclusão. É o link que indica que um conjunto inclui um subconjunto. Por exemplo, o conjunto múltiplos de 9 está incluído no conjunto múltiplos de 3.
- Pertencer. É a ligação entre um elemento e seu conjunto, ou seja, mostra que um elemento pertence a um conjunto. Por exemplo, o número 6 pertence ao conjunto múltiplos de 3.
- Não pertencimento. É o link que indica que um elemento não pertence a um conjunto. Por exemplo, o número 8 não pertence ao conjunto múltiplos de 3.
- Unión. É a formação de um novo conjunto que ocorre quando todos os elementos de um conjunto pertencem ao de outro e vice-versa. Por exemplo, os conjuntos livros de filosofia sim livros de literatura se unem para formar o todo livros de humanidades.
- Interseção. É o grupo de elementos que possuem características de dois ou mais conjuntos diferentes. Por exemplo, os números 12, 24, 36 estão na interseção, porque pertencem aos conjuntos múltiplos de 3 sim múltiplos de 4.
- Diferença. É o grupo de elementos que fazem parte de um conjunto, mas não de outro. Por exemplo, os números 3, 6 e 9 pertencem ao conjunto múltiplos de 3mas não para o todo múltiplos de 4.
- Complemento. É o grupo de elementos que não pertencem a um conjunto. Por exemplo, os números 1, 2 e 4 não fazem parte do conjunto múltiplos de 3.
História do diagrama de Venn
O diagrama de Venn surgiu em 1881, com a publicação de Lógica Simbólica, de John Venn, um matemático e lógico britânico. Nesse livro, o autor desenvolveu os diferentes tipos de gráficos que hoje são conhecidos, mas aplicados à representação de proposições que eram utilizadas na álgebra.
Os gráficos inventados por Venn têm vários antecedentes, mas os mais notáveis foram aqueles desenhados por Leonhard Euler, físico e matemático suíço. Venn simplificou os esquemas de Euler, pois propôs um único diagrama que com pequenas modificações poderia representar todas as proposições.
As principais diferenças entre o diagrama de Venn e o diagrama de Euler são:
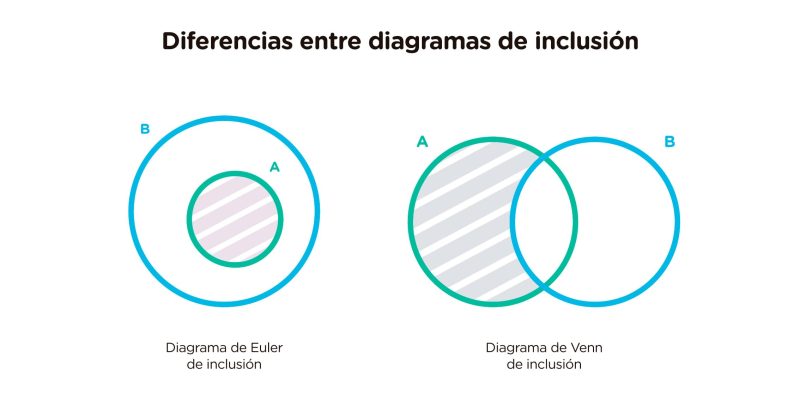
- O diagrama de Euler que representa a inclusão ou a proposição “Todo A é B” consiste em desenhar o círculo do conjunto A dentro do círculo do conjunto B. Já no diagrama de Venn, são desenhados dois círculos sobrepostos e o círculo está riscado. parte do conjunto A que não está incluída no conjunto B.
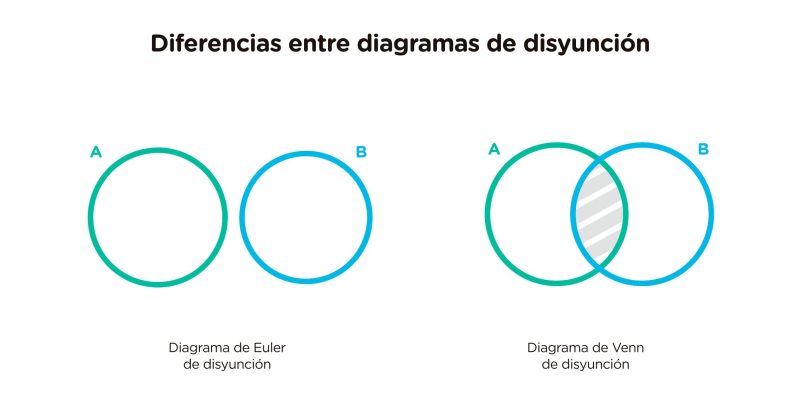
- O diagrama de Euler que representa a disjunção ou a proposição “Nenhum A é B” consiste em dois círculos separados. Por outro lado, no diagrama de Venn, a sobreposição dos círculos é riscada, de modo que é anulada.
- Continue com: Fluxograma
Referências
- Canela Morales, LA e Ruiz Sosa, FG (2019). Aspectos gerais do conhecimento simbólico e diagramático: o caso dos diagramas de Venn. Andaimes, 16(41), 63-85. https://doi.org/
- Cópia, IM e Cohen, C. (2013). Introdução à lógica. Limusine.
- Lipschutz, S. (1991). Teoria do conjunto e tópicos relacionados. McGraw-Hill.
- Ramírez, F. (2014). Cognotécnicas: Ferramentas para pensar mais e melhor. Alfa Ômega.